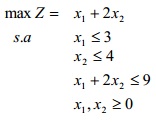Resolva numericamente usando o Solver.
1. A Fábrica de Rádios Sinval Vulah S.A. fabrica os modelos A, B e C que tem contribuição ao lucro de $16, $30 e $50, respectivamente. As exigências de produção mínima semanal são 20.000 para o modelo A, 120.000 para o modelo B e 60.000 para o modelo C. Cada tipo de rádio requer uma certa quantidade de tempo para fabricação das partes componentes, para a montagem e para embalagem. Especificamente, uma unidade do modelo A requer 0.3 horas para fabricar, 0.4 horas para montar e 0.1 para embalar. Os números correspondentes para uma unidade do modelo B são 0.4, 0.5 e 0.2, e para uma unidade do modelo C são 0.5, 0.8 e 0.3. Durante a próxima semana, a fábrica tem disponíveis 120.000 horas de tempo de fabricação, 160.000 horas de montagem e 48.000 horas de embalagem. Formule o modelo e resolva utilizando o Solver.
2. Uma fábrica de computadores produz dois modelos de microcomputadores A e B. O modelo A fornece um lucro de R$ 180,00 e B, de R$ 300,00. O modelo A requer, na sua produção, um gabinete pequeno e uma unidade de disco. O modelo B requer 1 gabinete grande e 2 unidades de disco. Existem no estoque 60 do gabinete pequeno, 50 do gabinete grande e 120 unidades de disco. Pergunta-se: Qual deve ser o esquema de produção que maximiza o lucro?
3. Uma empresa do ramo de madeira produz madeira tipo compensado e madeira serrada
comum e seus recursos são 40 m³ de pinho e 80 m³ de canela. A madeira serrada dá um
lucro de R$ 5,00 por m³ e a madeira compensada dá um lucro de R$ 0,70 por m³. Para produzir uma mistura de 1 metro cúbico de madeira serrada são requeridos 1 m³ de pinho e 3 m³ de canela. Para produzir 100 m³ de madeira compensada são requeridos 3 m³ de pinho e 5 m³ de canela. Compromissos de venda exigem que sejam produzidos pelo menos 5 m³ de madeira serrada e 900 m² de madeira compensada. Qual é o esquema de produção que maximiza o lucro?
4. Uma empresa tem três tipos de máquinas de processamento, tendo cada uma delas velocidade e taxas de defeitos diferentes. As máquinas do tipo I podem produzir 20 peças por hora com 5% de peças defeituosas; as do tipo II, 15 peças por hora com 10% de defeitos e as do tipo III, 10 peças por hora sem defeitos. O custo horário de operação por máquina é US$ 2,00; US$ 1,75 e US$ 1,50, respectivamente. Devem ser processadas 3500 peças por dia (8 horas/dia), mas só se dispõe de 8 máquinas do tipo I, 10 do tipo II e 20 do tipo III. Cada peça defeituosa custa à empresa US$ 1,00. Formule um modelo de PL para determinar a solução ótima para este problema.
5. Uma empresa petrolífera tem três refinarias (r = 1,2,3), e pretende distribuir combustíveis do tipo Y e Z para quatro mercados diferentes (m = 1,2,3,4). O custo de transporte do combustível Y é 2/3 do custo de transporte do combustível Z e ambos são diretamente proporcionais à distância. A demanda mensal de Y e Z para cada mercado é DYm e DZm respectivamente. A produção diária de Y e Z em cada refinaria é PYr e PZr, respectivamente.
Para um melhor uso da matéria-prima, cada refinaria deve produzir no mínimo 3 galões de Y para cada 2 galões do combustível Z. Formule um modelo de PL que minimize os custos de transporte e que, no caso de faltar combustível distribua a produção proporcionalmente à demanda.
6. Uma empresa petrolífera tem três refinarias (r = 1,2,3), e pretende distribuir combustíveis do tipo Y e Z para quatro mercados diferentes (m = 1,2,3,4). O custo de transporte do combustível Y é 2/3 do custo de transporte do combustível Z e ambos são diretamente proporcionais à distância. A demanda mensal de Y e Z para cada mercado é DYm e DZm respectivamente. A produção diária de Y e Z em cada refinaria é PYr e PZr, respectivamente.
Antes da distribuição, os combustíveis Y e Z deverão permanecer em estoque por pelo menos 15 e 20 dias, respectivamente. A capacidade total de estocagem de cada refinaria é limitada em Cr. Formule um modelo de PL que minimize os custos de transporte e que, no caso de faltar combustível distribua a produção proporcionalmente à demanda.
7. Um fundo de investimentos tem até R$ 300.000,00 para aplicar em duas ações. A empresa D é diversificada (tem 40% do seu capital aplicado em cerveja e o restante aplicado em refrigerantes) e espera-se que forneça bonificações de 12%. A empresa N não é diversificada (produz apenas cerveja) e espera-se que distribua bonificações de 20%. Para este investimento, considerando a legislação governamental aplicável, o fundo está sujeito às seguintes restrições:
a) O investimento na empresa diversificada pode atingir R$ 270.000,00.
b) O investimento na empresa não-diversificada pode atingir R$ 150.000,00.
c) Em cada produto (cerveja ou refrigerante) pode-se investir até R$ 180.000,00.
b) O investimento na empresa não-diversificada pode atingir R$ 150.000,00.
c) Em cada produto (cerveja ou refrigerante) pode-se investir até R$ 180.000,00.
Pede-se: Qual o esquema de investimento que maximiza o lucro?
8. Uma empresa aérea deseja comprar aviões a jato grandes, médios e pequenos. O preço de compra é de US$ 33,5 milhões para cada avião grande, US$ 25,0 milhões para cada avião médio e US$ 17,5 milhões para cada avião pequeno. O conselho diretor autorizou um comprometimento máximo de US$ 750 milhões para esta compra. Qualquer que seja a compra realizada, espera-se que haja mercado para assegurar a utilização dos aviões em sua capacidade máxima. Se estima que os lucros anuais líquidos (descontando o custo de recuperação do capital aplicado), é de US$ 2,1 milhões para um avião grande, US$ 1,5 milhões para um avião médio e US$ 1,15 milhões para um avião pequeno.
Supõe-se que a empresa poderá dispor de pilotos treinados para operar até 30 aviões novos.
Se forem comprados apenas aviões pequenos, as instalações de manutenção poderiam comportar até 40 aviões, porém cada avião médio equivale a 1¼ aviões pequenos e cada avião grande equivale a 1¾ aviões pequenos, em termos de utilização das mesmas instalações de manutenção. Formule um modelo de programação inteira para este problema.
9. A diretora de pessoal de uma empresa de aviação comercial deve decidir quantas aeromoças deverão ser treinadas e contratadas nos próximos seis meses. As necessidades, expressas pelo número de aeromoças-horas-de-voo são as seguintes: 8.000 em janeiro; 9.000 em fevereiro; 7.000 em março; 10.000 em abril; 9.000 em maio; e 11.000 em junho.
Leva um mês de treinamento antes que uma aeromoça possa ser posta em um voo regular; assim, uma garota deve ser contratada pelo menos 1 mês antes que ela seja realmente necessária. Cada moça treinada requer requer 100 horas de supervisão de uma aeromoça experiente durante o mês de treinamento, de modo que são disponíveis 100 horas a menos para o serviço de voo por aeromoças regulares.
Cada aeromoça experiente pode trabalhar até 150 horas em um mês, e a empresa dispõe de 60 aeromoças no começo de janeiro. A política da empresa é não demitir ninguém.
Porém, no fim de cada mês, aproximadamente 10% das aeromoças pedem demissão para se dedicarem a outras atividades e para se casarem. Uma aeromoça experiente custa a empresa R$ 1.500,00 por mês, enquanto que na fase de treinamento o custo é de somente R$ 900,00 (já incluindo os encargos legais).
10. Formule um modelo de programação linear para determinar a política ótima de contratação e
treinamento da empresa, e utilize um pacote de programação linear para obter a solução ótima. Interprete a solução encontrada.
Uma companhia de transporte resolveu adquirir uma nova frota de caminhões para o que dispõe de R$ 4.000.000,00. Existem no mercado três modelos de caminhões que podem ser adquiridos: A, B e C.
O caminhão A pode receber até 10 toneladas de carga, tem uma velocidade média de 56 km/h e custa R$ 80.000,00; B tem uma capacidade de 20 toneladas e uma velocidade média de 48 km/h, seu custo e R$ 130.000.00; C é provido de leito para o ajudante de motorista e, por isso, embora seja semelhante a B, a sua capacidade é de 18 toneladas e seu custo é de R$ 150.000.00.
O caminhão A é operado por uma só pessoa e, se for utilizado em três turnos, pode rodar 18 horas por dia.
Os caminhões B e C exigem e pessoas; enquanto B pode rodar 18 horas por dia, no regime de três turnos, C pode trabalhar 21 horas por dia.
A companhia dispõe de 150 motoristas; as possibilidades de obter mais são muito reduzidas.
Por outro lado, as disponibilidades de manutenção limitam a nova frota a um máximo de 30 veículos.
Pede-se que se estabeleça um modelo de programação linear destinado a determinar quantos veículos de cada tipo devem ser adquiridos, de modo que a capacidade da frota em ton.km por dia seja máxima. Resolva o problema e interprete a solução obtida.